DP Bora - transformation-based optimizers strike back!

GitHub repository

Introduction

DP Bora is a novel algorithm for optimization of SQL queries. It is closely based on DP SUBE, so readers are advised to read the DP SUBE paper first (On the correct and complete enumeration of the core search space). DP Bora dispoves three thesis present in DP SUBE paper:

1. Transformation-based optimizers are not efficient because they consume a lot of memory
2. Transformation-based optimizers generate exponential number of duplicates
3. Transformation-based optimizers generate invalid transformations that are discarded later

Current limitations are overcome by innovative data structure called query hypertree, which describes complete combinatorial search space in a compact and duplicate-free representation suitable for use in both top-down (memoization) and bottom-up (dynamic programming) optimizers.

DP Bora enumerates complete search space (all possible bushy trees) and supports arbitrary joins and arbitrary predicates. Extension of DP SUBE is that arbitrary transformations are also supported by the algorithm and it’s main internal data structure.

DP Bora comes with a reference implementation to alleviate all possible ambiguities present in the text and to provide additional information necessary for production-grade implementation.

Author strongly believes that complex (i.e. hard to understand and truly prove) mathematical proofs and absence of reference implementations lead to general disregard to computer science from industry-oriented team members. DP Bora aims to overcome discrepancy between theory and practice.

Query hypertree

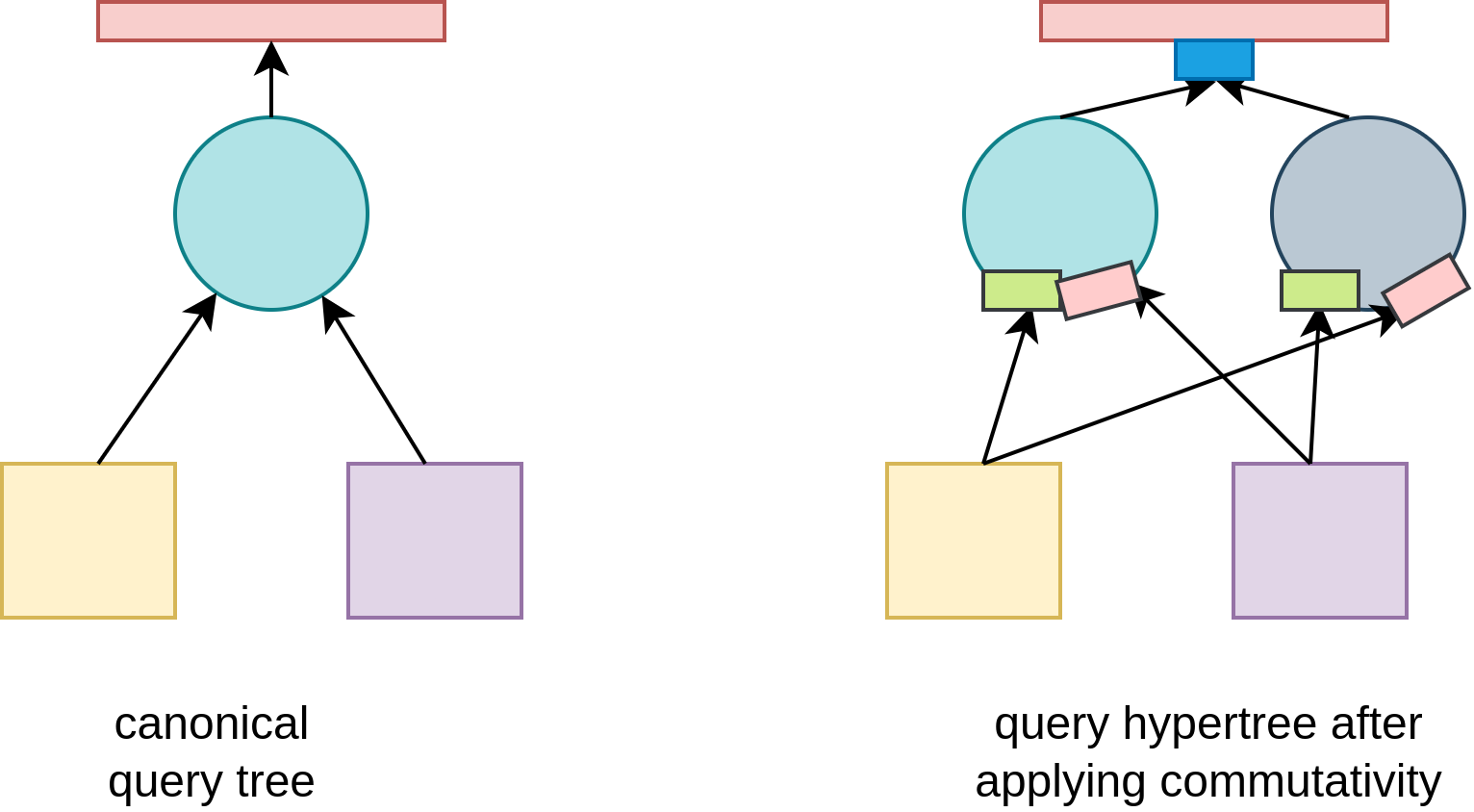
Query hypertree presents a generalization of canonical query tree. Every node has associated operator and sets of possible left and right inputs. Inputs are always a function over a set of originating relations. Every member of input sets is a valid function that has an equivalent output result.

Every path taken in the query hypertree is valid, and problem query optimization is equivalent to finding the path with the lowest cost. Every node has it’s cost function based on output parameters from input costs. To find the lowest cost, it is necessary to find lowest cost left and right inputs. For every element of the according input set, cost is calculated, and the lowest cost element is selected.

As DP Bora constructs valid paths only, main premise of dynamic programming that every sub-solution of an optimal solution is optimal, caching results using memoization or DP table is possible.

Algorithm outline

1. Canonical query tree is constructed directly from the SQL query
2. All initially present operator nodes are addded to the worklist
3. For every node in the worklist, every possible transformation is attempted
4. Transformation output is stored in query hypertree as an alternative path that does not affect originally present paths
5. After performing all possible transformations, a node is removed from the worklist
6. All newly created (i.e. transformed) nodes are added to the worklist
7. If a transformation attemts to create a node that is present, existing equivalent node is reused
8. Nodes are considered equivalent if they have the same operator and same input relations on the left side and on the right side
9. When worklist becomes empty, complete search space was enumerated
10. Query hypertree is used to calculate the cheapest path using either memoization or dynamic programming

Supported transformations and node equivalence

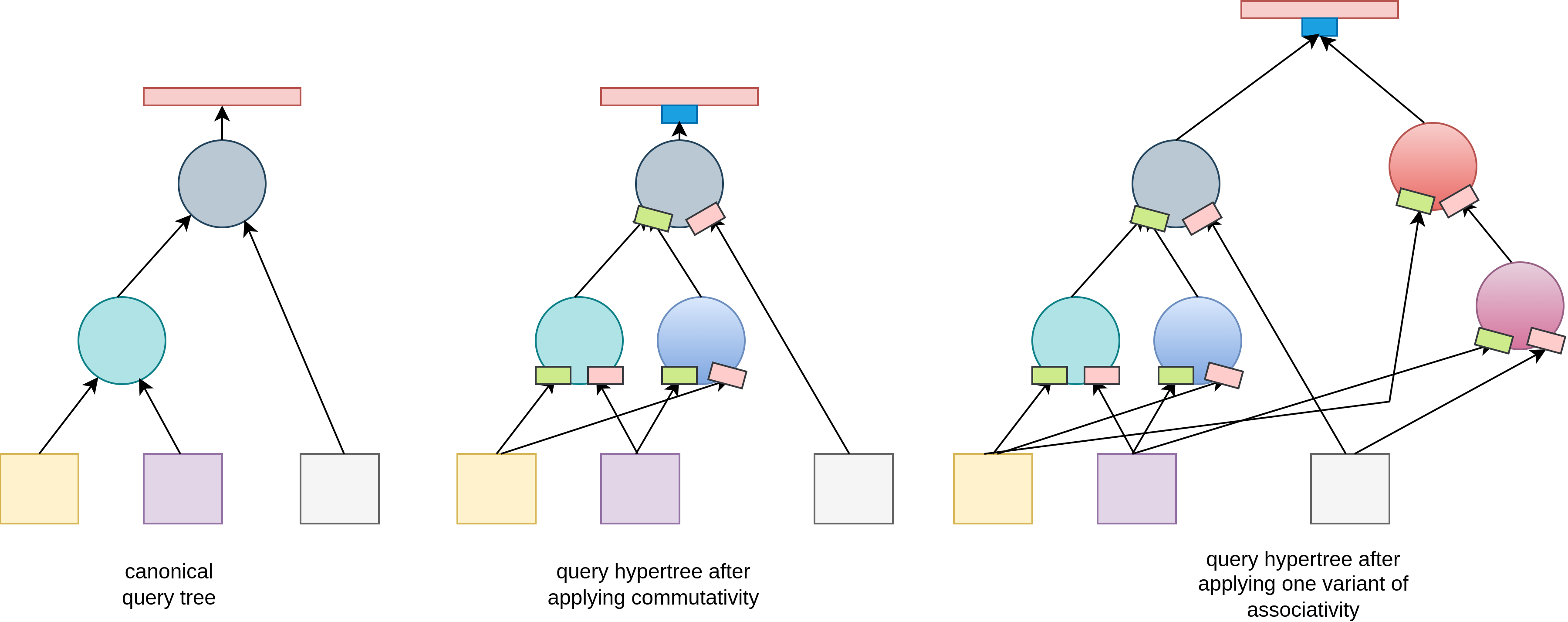
DP Bora supports all transformations described in the DP SUBE paper: commutativity, associativity, l-asscom and r-asscom. DP Bora uses the same matrices and predicates from DP SUBE paper to check whether a transformation can be applied to a subtree. DP Bora does not use conflict representation set calculation.

Instead, transformations are applied (if possible) and added as possible alternative paths in the query hypertree. Instead of resolving conflicts, DP Bora attemts all possible transformations over all possible paths using duplicate-prevention strategy based on operator equivalence.

Separate map-based structure holds pairs of tuples (operator, left_relation_set, right_relation_set) and query hypernodes. When a transformation attemts to create a node, equivalent_nodes map is searched for existence of the needed node. If needed node exists, it is picked. Otherwise, a new node is constructed and added to the equivalent_nodes map. Left and right inputs are stored as sets, so adding duplicate paths is prevented as well. Using reference/memory address equivalence in sets is sufficient, as duplicate construction (previous step) is prevented using a robust approach.

DP Bora can be extended to support arbitrary node transformations as long as they can support duplicate prevention mechanisms described above.

Worklist item processing

For transformations that need to examine only one operator node (i.e. commutativity), only operator applicability and equivalent node existence need to be performed.

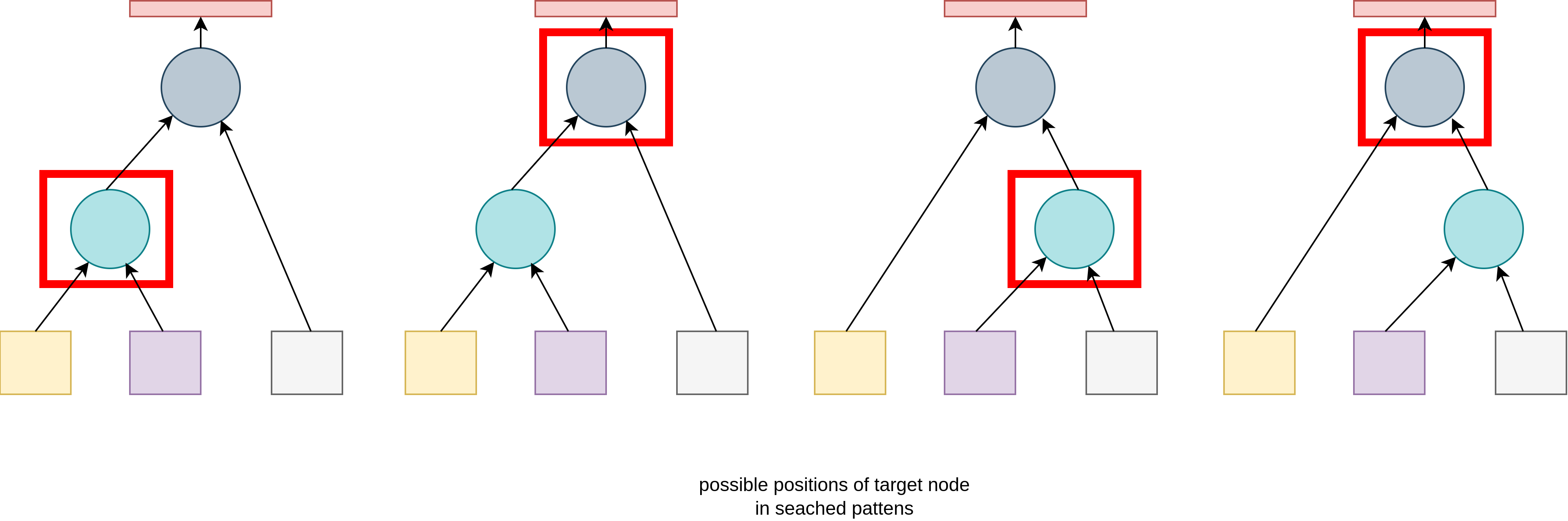
For transformations that examine two operator nodes (i.e. associativity, l-asscom and r-asscom), a more sophisticated analysis is required. Need for this arises from the fact that when analyzing subtree hierarchy, we can be looking at either the left or the right operator present in the same searhed pattern.

This problem is not present in the first pass that analyzes canonical tree, but is necessary in other successive passes, as in general case it is not possible to know in which direction should transformation be attempted, so all possibilities need to be taken into account.

Applying generalized transformation to hypernodes and hypertrees

DP Bora applies same transformations described in the DP SUBE paper, but in a generalized form that supports hypernodes and hypertrees. The essence of transformation generalization is that if one node can have multiple equivalent input and output paths, all transformed nodes must be connected properly to all possible paths.

All hypernodes store pointers to parent nodes, besides pointers to child nodes. This means that hypertree is implemented using a doubly-linked approach. As left and right inputs are distinct sets (to preserve original query semantics), left and right parent pointers are stored separately as well. This enables detecting position of a node in the searched pattern when looking from the child perspective (shown on the image in the previous section). Additionally, hypernodes store a top pointer for all single input parent nodes (currently, this is only used for pointer to top parent result node, but can be used for sort operators if logical and physical plan generation is unified).

Generalized transformations that are applied only on one hypernode (i.e. commutativity) only need to check whether the transformation is applicable. If that is the case, a new hypernode is created and linked as an alternative input to all parents of the original node.

In generalized commutativity, whole left and right input sets are switched, which is a generalization of switching only single left and right input relations/subtrees.

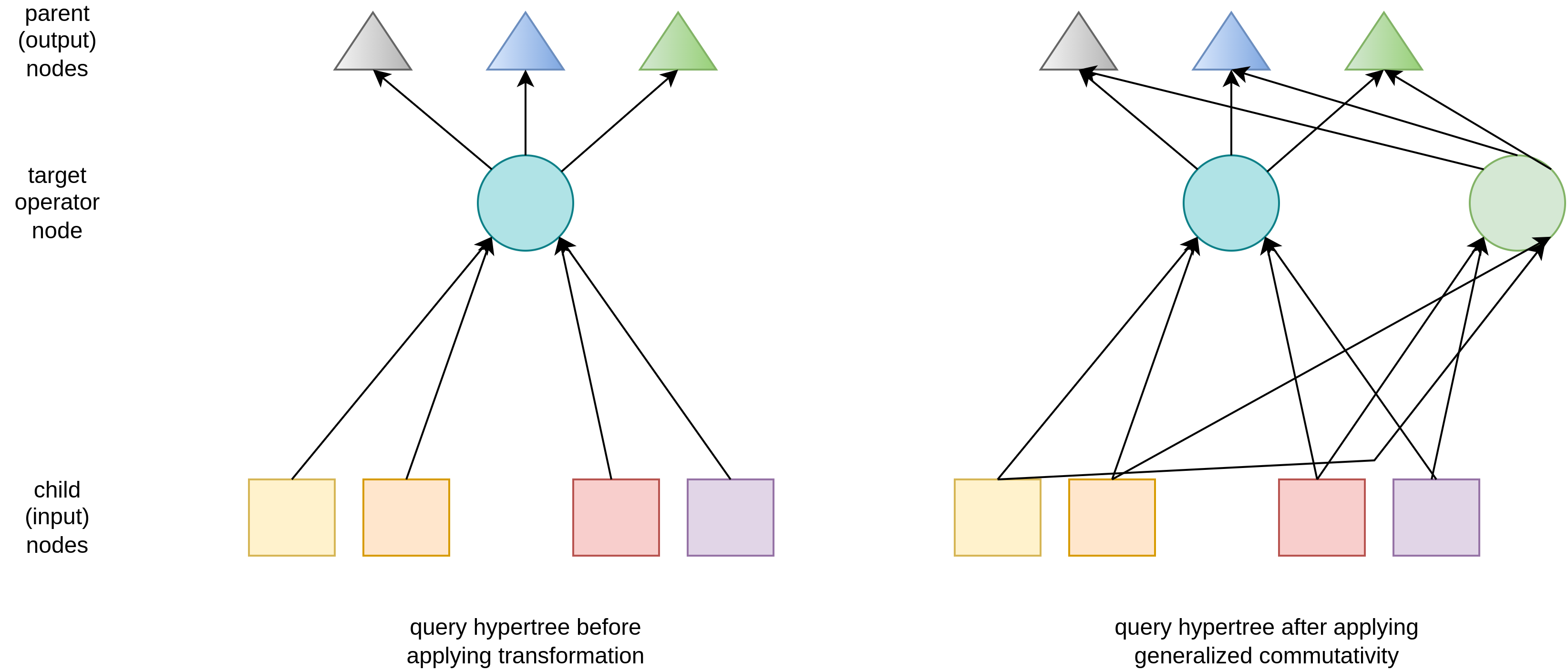
Generalized transformations that are applied on two hypernodes (i.e. associativity, l-asscom and r-asscom) are more sophisticated and abstract. Transformation applicability is checked for every left/right input/output node of the local subtree. If operation is applicable, new nodes are connected to existing input and output leaf sets. Internal link is not copied as different input paths need separate examination of applicability. On the image, hexagon denotes input operator node which is not associative, so it remains on the original position and does not get transformed.

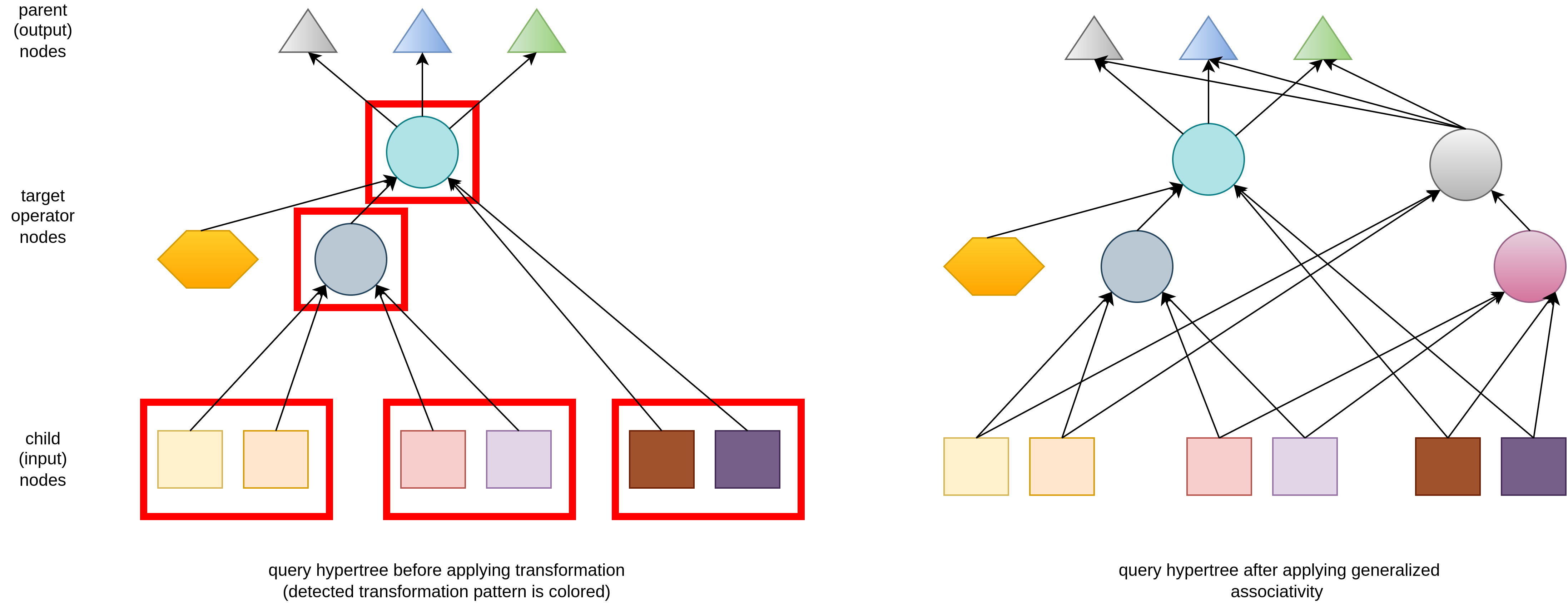
Generalized l-asscom and r-asscom are implemented using the same approach as generalized associativity. The only difference is that leaf inputs are interconnected in different order.

Generalized transformations work in a context-free manner and do not need to examine whole hypertree to determine transformation applicability. Transformation applicability is decided by a function that needs only operator, left and right input relations sets and predicate (needed for checking whether the predicate rejects null, which is neccessary for applicability in cerain cases from DP SUBE tables). One hypertree transformation can create combinatorially large number of possible new paths in time and space efficient manner.

Unification and stratification of physical plan generation

Reference implementation works only on logical operators. To implement a production-grade optimizer based on DP Bora, logical operators must be transformed to physical operators. Sorting of input always affects both the cost and possible applicability of physical operators (i.e. merge join and it’s derivatives). It is possible to extend DP Bora to add necessary sort operators to alternate query hypertree paths using either unified (i.e. generate all physical plans in one step) or stratified (i.e. generate possible physical plans after all logical plans) approach.

Restriction of the search space

DP-based algorithms over bushy trees provide absolute optimal query plans, assuming that cost functions (and mainly cardinality estimators) are sufficiently precise. However, they take exponentially more steps as the number of input relations grows. Many heuristics for transforming canonical trees based on detected query patterns (such as star queries) exist.

It is possible to modify DP Bora to restrict search space by restricting applied transformation as the number of input relations grows, as the list of transformations is configurable. However, picking needed transformations still remains a heuristic, but DP benefits are not completely discarded. Practical applicability of such approach needs further analysis.